合成梁とは何でしょうか?構造設計をしていると必ず耳にする言葉でしょう。学生時代は聞いたことがありませんでした。(講義を聞いてなかっただけかも知れませんが💦)
必ずと言って設計で使用するので覚えておきましょう!
間違いやすい箇所・気を付けるべき箇所についても解説します。
合成梁とは?
合成梁とは鉄骨梁の上部に取り付くコンクリートスラブによる剛性の割増しを考慮した梁のことです。
合成梁とするにはコンクリートと鉄骨梁が一体的であることを確認する必要があります。具体的にはスタッドでコンクリートと鉄骨梁を一体化します。
メリットは鉄骨小梁の設計の記事で書いてありますが、たわみで断面が決まってしまう小梁に対して剛性割増を考慮することで断面を小さくすることができます。
つまり、鉄骨数量の削減・コストの削減に!!!

合成梁の設計方法
次に合成梁の設計方法を示します。
具体的には合成梁とするために必要なスタッド本数の設計、それに応じた鉄骨梁の剛性割増率を算定します。
上記の図のように鉄骨梁とRCスラブを一体化することで合成梁として鉄骨梁の合成割増を考慮できるため、スタッドによってせん断力が伝達できることを確認することが必要となります。
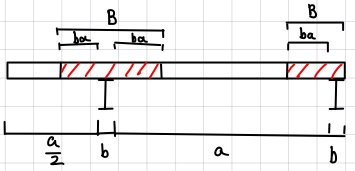
①有効幅B
・両側スラブ B=2ba+b
・片側スラブ B=ba+b
B:スラブの有効幅(mm)
b:鉄骨梁の上フランジ幅(mm)
②協力幅ba
・ラーメン・連続梁の場合
ba=(0.5-0.6・a/l)a a<0.5lの場合
ba=0.1l a≧0.5lの場合
l:ラーメンまたは連続梁のスパン
a:下記図参照
・単純梁の場合
ba=(0.5-0.3・a/lo)a a<loの場合
ba=0.2lo a≧loの場合
lo:単純梁のスパン
③断面2次モーメント,断面係数
正曲げモーメントを受ける場合
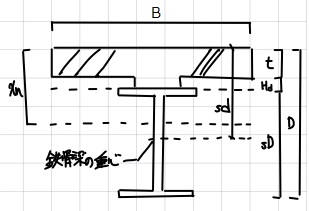
pt=sa/(B・sd) sa:鉄骨梁の全断面積[mm2]
t1=t/sd t:スラブのせい[mm]
n:ヤング係数(10:剛比算定用(普通コンクリート)
15:断面算定)
sd:コンクリート圧縮縁から鉄骨梁の重心までの距離[mm]
中立軸はスラブ内
条件:Pt<t1^2/(2n(1-t1))
中立軸位置:xn=n・pt(1+2/(n・pt)-1)^1/2*sd
断面2次モーメント:cIn=B・xn^3/(3n)+sI+sa(sd-xn)^2
xn :正曲げ時のコンクリート上縁から中立軸までの距離[mm]
cIn:正曲げを受ける合成梁の有効等価断面の断面2次モーメント[mm4]
sI :鉄骨梁の断面2次モーメント[mm4]
中立軸はスラブ外(通常はこの範囲)
条件:Pt≧t1^2/(2n(1-t1))
中立軸位置:xn=(t1^2+2n・pt)/(2(t1+n・pt))*sd
断面2次モーメント:cIn=B・t/n(t^2/12+(xn-t/2)^2)+sI+sa(sd-xn)^2
スラブ上端位置と鉄骨梁下端位置の断面係数[mm3]
cZc:スラブ上端側の有効等価断面係数[mm3]=n*cIn/xn
cZt:鉄骨梁下フランジ側の有効等価断面係数[mm3]=cIn/(D-xn)
D:合成梁の全せい[mm]
負曲げモーメントを受ける場合→他記事にて説明します
通常、小梁などは負曲げを受けません。
断面二次モーメント、断面係数は通常の鉄骨と同じとし割増はないもので考えます。
断面2次モーメント,断面係数
最終的には正曲げの場合と負曲げの場合の平均を断面二次モーメント、断面係数とします。
不完全合成梁の断面係数,断面2次モーメント
スタッド数により完全合成梁とならず不完全合成梁として設計する場合があります。注意!!!
その際は上記の計算より小さい値となるため、確認しておくことが大切です。
不完全合成梁のスタッドの設計については他記事にて説明したいと思います。
算定例

まとめ
本記事では合成梁について説明しました。
合成梁で計算することで経済的な構造設計を行うことができます。スラブによる剛性割増しを考慮する事で鉄骨断面を小さくする事ができるからです。
鉄骨の数量を削減したいときは合成梁として設計する事で満足できる事が多いので忘れずに覚えておきましょう。
 | 価格:10,476円 |


