本記事では露出柱脚(在来工法)について説明します。
柱脚の種類は露出柱脚、根巻柱脚、埋込柱脚の三種類があります。
本記事で説明する露出柱脚は三種類の中で最も固定度が小さく、簡易なものです。
一次設計(許容応力度設計)
固定度の算定

露出柱脚の固定度はアンカーボルトの引張側本数が多いほど、位置が外側にあるほど大きくなります。
そして、アンカーボルトの長さが大きいほど固定度は小さくなります。
アンカーボルトの長さは定着長さより一般的に決まります。
定着長さはアンカーボルト径dにより、20d~30d程度とするのが一般的です。
ここで重要なことは固定度が変わると設計用応力Mなどが変わってしまうということです。
設計用応力を満足しないからといって安易にアンカーボルト本数を増やしたりすると固定度が上がり、設計用応力も大きくなってしまうため注意が必要です。
設計用応力の算定
次に設計用応力を求めます。
先ほど求めた固定度を一貫計算に入力し、一貫計算を行うと柱脚の設計用応力が求まります。
断面算定
コンクリートの圧縮応力度
設計用応力N・Mよりベースプレートに作用する反力を求めます。
このとき偏心量e=M/Nより中立軸の位置を求める必要があります。
①中立軸がベースプレートの外の場合(e<D/6)
σc=N/BD(1+6e/D)
②中立軸がベースプレート内でアンカーボルトより外の場合(D/6<e<D/6+dt/3)
σc=2N/(3B(D/2-e))
③中立軸がベースプレート内でアンカーボルトより内の場合 (D/6 +dt/3 <e)
σc=2N(e+(D/2)-dt)(B・xn(D-dt-(xn/3)) )
xnは下図より求めることが出来ます。

最後にσc≦fc fc:コンクリートの許容圧縮応力度 を満足することを確認します。
アンカーボルトの引張力
アンカーボルトの引張力は上のコンクリート圧縮応力度との釣り合いより求めます。
T=N(e-(D/2)+(xn/3))/(D-dt-(xn/3))
必要な断面積はat≧T/ft より求めます。
ベースプレートの曲げ応力
上記の圧縮応力および引張力がベースプレートに作用した場合の曲げモーメントに対してベースプレート厚が満足することを確認します。
圧縮応力はスラブの算定と同様に分布荷重が作用した場合についてMを求めます。
リブプレートまたはフランジ・ウェブで囲まれた二辺固定、三辺固定として計算を行います。
t≧√(6M/fb)
引張力に対してはアンカーボルトから柱フランジの距離g×引張力TよりMを求めます。
断面係数は幅be=R+2g(R:アンカーボルト径)、ベースプレート厚さtよりZ=be・t^2/6で求めます。
t≧√(6M/(fb・be))
リブプレートのせん断応力
リブプレートは下面の反力σcを鉄骨柱に伝達するための部材です。
リブプレートの負担面積Aはリブプレートの配置方法により異なります。
負担する力Rr=A×σcより求めます。
M=Rr×br/2(br:リブプレートとベースプレートが接している面の幅)
σb=M/Z≦ft、τ=1.5Rr/(hr・tr)≦fs ( hr:リブプレートと柱が接している面の幅 )
Z=tr・hr^2/6
溶接の設計
リブプレートと柱の溶接
曲げ応力度:p1=M/(2×0.7s・L1^2/6)≦fw (L1:hr部分の溶接長さ)
せん断応力度:p2=Rr/(2×0.7s・L1)≦fw (L1:hr部分の溶接長さ)
√(p1^2+p2^2)≦fw
リブプレートとベースプレートの溶接
p3=Rr/(2×0.7s・L2)≦fw (L2:br部分の溶接長さ)
幅圧比 br/tr<240√F を満足することを確認すること。
ベース下面のせん断力
摩擦伝達の場合
Q≦0.4(N+T)
上記を満足しない場合、アンカーボルトに負担させます。
Q≦ag・fs を満足させる必要があります。
不足分だけアンカーボルトに負担させる考え方もありますが、どのように力が伝達するかは設計者判断によるところが大きいです。
二次設計
露出柱脚の設計フロー
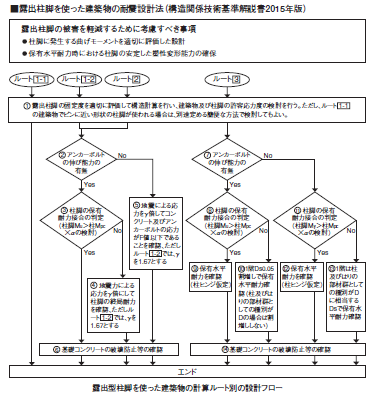
上記の設計フローは鋼構造設計便覧P8-53に記載されております。
二次設計の詳細については他の記事に書いていこうと思いますので、そちらを参考にして下さい。
また、設計例についても他の記事で書いていきますので参考にして下さい。
まとめ
本記事では露出柱脚の設計方法について書きました。
ベースプレート、アンカーボルト、リブプレート、基礎コンクリートの設計が必要になります。
アンカーボルト径とベースプレート厚は近い値になることが多いです。


